
Coding a Simple Recommendation System in R
When we shop online, we often get recommendations for other products that are similar to ones we’ve been looking at. Systems that recommend related products and services are frequently referred to as recommendation systems.
In today’s Code Lab, we’ll code a simple recommendation system using something called cosine similarity! We’ll test our system on a small dataset on the nutritional content of food items from McDonald’s.
Here’s a preview of how our simple recommender system will work. We’ll start with a particular food item. Our goal is to get a list of the top most similar food items among all the other food items in our nutritional dataset. To find the most similar food items, we’ll compute the cosine similarity between our chosen food item and all the other items in the nutritional database. Finally, we’ll return the items that were most similar to our chosen food item.
Let’s begin by loading our data into R!
Loading our nutritional content data into R

We’ll use the read.csv() function to load the data into R. Since the first row of the data contains the variable names, we will use the header=TRUE option inside the read.csv() function.
## Load our nutrition dataset
nutrition <- read.csv("mcd_nutrition.csv", sep=',', header=TRUE)It’s always a good idea to take a look at your data to make sure it loaded as you expected. So let’s use the head() function to look at the first few lines of our nutrition data.
## Look at first few lines of our nutrition dataset
head(nutrition)
#> name calories
#> 1 Triple Cheeseburger 520
#> 2 Cheddar Bacon Onion Grilled Chicken Sandwich 360
#> 3 Bacon Clubhouse Burger 730
#> 4 Double Filet-O- Fish 540
#> 5 Premium Buttermilk Crispy Chicken Bacon Clubhouse Sandwich 780
#> 6 Buffalo Ranch McChicken 360
#> calories_fat total_fat tf_pd saturated_fat sf_pd trans_fat cholestrol chol_pd
#> 1 250 28 43 14 68 1.5 110 37
#> 2 160 18 28 8 42 0.0 155 52
#> 3 370 41 63 16 80 1.5 125 42
#> 4 230 26 40 6 29 0.0 80 27
#> 5 350 39 61 11 54 0.0 110 37
#> 6 140 16 25 3 16 0.0 40 13
#> sodium sdm_pd carbs carbs_pd diet_fiber df_pdf sugars protein vitA vitC
#> 1 1180 49 35 12 2 8 7 32 20 2
#> 2 1600 67 6 2 1 3 2 44 6 30
#> 3 1280 53 49 16 2 9 12 40 20 20
#> 4 790 33 47 16 2 8 5 28 10 0
#> 5 1550 64 68 23 4 16 12 40 20 25
#> 6 800 33 39 13 2 9 5 15 4 2
#> calcium iron
#> 1 20 25
#> 2 15 4
#> 3 20 25
#> 4 10 10
#> 5 20 15
#> 6 2 15The first column in nutrition contains the names of the food items. Since this is not a numeric variable, let’s separate it from the rest of the nutritional data. To do that, let’s store the names of the food items in a variable called items. Let’s also store the rest of the nutritional data in a matrix called X.
X <- as.matrix(nutrition[,-1])
items <- nutrition$namePreparing our nutritional data
Now that we’ve loaded our data into R, let’s work on preparing our data. A quick look at our data with the head() function above showed us that the nutritional variables are recorded using different scales. We see, for example, that since sodium is listed in milligrams, the numbers for sodium are much larger in scale than numbers for variables listed in grams. If we don’t account for the differences in scales, the similarity between fast food items will be dominated by the variables containing large numeric values.
To address the differences in scales, let’s first standardize the nutrition variables. This will make sure that each nutrition variable carries the same weight when we compute the similarity between food items later.
Standardizing the nutritional variables
Let’s use the notation \(\mathbf{X}_{(:,j)} \in \mathbb{R}^{202}\) to indicate the \(j^{th}\) column of \(\mathbf{X}\). We’ll also refer to this as the \(j^{th}\) nutrition vector.
To standardize the \(j^{th}\) nutritional variable, we will first subtract the variable mean \(\bar{x}_{j}\) from every entry in the variable \(\mathbf{X}_{(:,j)}\). Then we will divide each entry in \(\mathbf{X}_{(:,j)}\) by its standard deviation \(\hat{\sigma}_{j}\).
Let’s call the resulting standardized variable \(\mathbf{Z}_{(:,j)} \in \mathbb{R}^{202}\). Then we compute it as follows
\[\mathbf{Z}_{(:,j)} = \frac{1}{\hat{\sigma}_{j}}\left[\mathbf{X}_{(:,j)} - \bar{x}_{j}\mathbf{1}\right].\]In the equation above, we’ll need to compute the variable mean \(\bar{x}_{j}\). We compute it as
\[\bar{x}_j = \frac{1}{202}\left [\mathbf{X}_{(1,j)} + \mathbf{X}_{(2,j)} + \cdots + \mathbf{X}_{(202,j)} \right] = \frac{1}{202}\mathbf{1}_{202}^{T}\mathbf{X}_{(:,j)},\]where the notation \(\mathbf{X}_{(i,j)}\) refers to the entry in the \(i^{th}\) row and \(j^{th}\) column of \(\mathbf{X}\). The portion after the first equal sign is the formula for computing the mean that you typically see. The part after the second equal sign is an inner product.
Do you remember how we discussed the inner product in our post on getting started with linear algebra in R? Another way to write the sum of all the entries in \(\mathbf{X}_{(:,j)}\) is to write it as inner product between the all ones vector of length 202 (this is the vector of length 202 whose entries are all \(1\)) and the \(j^{th}\) column of \(\mathbf{X}\).
The second item we’ll need to compute is the standard deviation of the \(j^{th}\) variable. We denote this with \(\hat{\sigma}_{j}\) and compute it as
\[\hat{\sigma}_j = \sqrt{\frac{1}{202 - 1}\sum_{i=1}^{202} (\mathbf{X}_{(i,j)} - \bar{x}_{j})^2}.\]This means that for each entry in the \(j^{th}\) column of \(\mathbf{X}\), we will subtract the column mean and square the resulting number. Then we will sum up all the squared numbers and divide that sum by \(\frac{1}{n-1}\). Finally, we will take the square root of the whole thing.
We could write some functions to compute these two items but it turns out that R already has a function called scale() that we can use for performing these two steps. Let’s apply the scale() function to \(\mathbf{X}\) and then store the resulting matrix with standardized columns in the matrix \(\mathbf{Z}\).
Z <- scale(X, center = TRUE, scale = TRUE)Normalizing the food items in the standardized variables
Each row in \(\mathbf{Z}\) is an observation (or different food item) in the standardized nutritional data. To make sure that all the food items carry the same weight, let’s normalize them so that they all have unit length. That means that we will divide each row by its length so that each row has length \(1\). (For a brief refresher on distance and the Euclidean norm, please see our post on getting started with linear algebra in R.)
We can use the norm() function to compute the Euclidean norm of each row in \(\mathbf{Z}\). Since R does not have a norm function for vector inputs, we will tell R to treat the vector as a matrix with as.matrix(). We’ll also specify the parameter type="F" to specify that we want R to use the Frobenius norm for matrices, which is the matrix version of the Euclidean norm for vectors.
Since we want to divide each observation by its Euclidean norm, let’s write a function called normalize to do this.
Now that we have a function for scaling each observation, we can apply it to every row in \(\mathbf{Z}\). We can use the apply() function in R to apply a function across every row (or column) in a matrix. A quick look at the help documentation for apply() with ?appply shows us how to use this function. Our first input in the apply() function is our matrix \(\mathbf{Z}\). This tells R that we want to apply a function to the rows or columns of \(\mathbf{Z}\). The second input is 1. This tells R that we want to apply the function along the rows of \(\mathbf{Z}\) (rather than its columns). The third input is the actual function that we want to apply to \(\mathbf{Z}\).
In the code snippet above, we’ve taken the transpose of the output from apply() with t() so that the dimensions match our original dimensions for the standardized variables \(\mathbf{Z}\).
dim(Z)
#> [1] 202 21We can check to make sure that we’ve normalized our food item vectors by computing their lengths. If they are normalized, then they should each have length equal to \(1\). Just to check our work, let’s use the apply() function again on the rows of \(\mathbf{Z}\) to compute their row lengths.
apply(Z, 1, FUN=function(x){norm(as.matrix(x),"F")})
#> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [38] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [149] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#> [186] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1Writing a function to find the index of our chosen food item
Now that we’ve standardized our nutritional variables and normalized our food items, we’re ready to compute the similarities between the different food items!
Let’s start by writing a function to find the index, or position, of our chosen food item in items. Let’s call this function get_index. This function will take in the name of our chosen food item and it will return the index of our chosen food item in index.
Let’s try this on your own first! What would you fill in the body of the get_index function below? (Hint: We can use the which() function in R to return the index of our food item in items.)
In the code snippet below, we’ve added comments above our function to tell the user what the function is for, and what inputs it takes in. Remember that R won’t read anything after the # so we can make comments to ourselves and other users of our code by adding a # before any text.
The @param indicates the parameters that our function takes in. The first object after @param is the name of the parameter. This name matches the parameter input in the function. The text following that object gives us some more information about the parameter but is not actually used by R.
#' Get index of our chosen food item
#'
#' @param items Names of food items
#' @param our_item Our chosen food item
get_index <- function(items, our_item) {
# TRY THIS ON YOUR OWN FIRST
}
Now let’s work on this together! Does your code look something like the following?
#' Get index of our chosen food item
#'
#' @param items Names of food items
#' @param our_item Our chosen food item
get_index <- function(items, our_item) {
# Return index of our chosen food item in `items`
return(which(items == our_item))
}Let’s test out our get_index function! What is the index of “Berry Bran Muffin”?
ix_berry_muffins <- get_index(items, "Berry Bran Muffin")
ix_berry_muffins
#> [1] 184Let’s check to make sure that this is the same index that “Berry Bran Muffin” has in our nutrition data. We can do this by grabbing the item in nutrition that corresponds to the index that we computed for “Berry Bran Muffin”.
nutrition[ix_berry_muffins,]
#> name calories calories_fat total_fat tf_pd saturated_fat sf_pd
#> 184 Berry Bran Muffin 410 140 15 23 1.5 8
#> trans_fat cholestrol chol_pd sodium sdm_pd carbs carbs_pd diet_fiber df_pdf
#> 184 0 0 0 480 20 62 21 7 27
#> sugars protein vitA vitC calcium iron
#> 184 28 7 0 0 6 15Great! Our get_items function got the correct index for “Berry Bran Muffin”! Let’s try another example! What is the index of “Green Chile Bacon Burrito”?
ix_green_chile_bacon <- get_index(items, "Green Chile Bacon Burrito")
ix_green_chile_bacon
#> [1] 201Did we get the correct index for “Green Chile Bacon Burrito”? Let’s find out by grabbing the item corresponding to ix_green_chile_bacon in nutrition!
nutrition[ix_green_chile_bacon,]
#> name calories calories_fat total_fat tf_pd
#> 201 Green Chile Bacon Burrito 690 310 35 53
#> saturated_fat sf_pd trans_fat cholestrol chol_pd sodium sdm_pd carbs
#> 201 12 61 1 410 137 1640 68 66
#> carbs_pd diet_fiber df_pdf sugars protein vitA vitC calcium iron
#> 201 22 3 14 5 29 20 40 30 25Computing similarity between food items with inner products
Now we’re ready to use cosine similarity to recommend other food items in items that are most similar to our chosen food item! Before we dive into our coding, let’s talk a bit about cosine similarity.
Remember how we discussed inner products in our post on getting started with linear algebra in R? It turns out that we can use inner products to compute how similar two vectors are to each other. To see this, let’s consider the following two vectors
\[\mathbf{v} = \begin{pmatrix}v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{pmatrix} \quad \text{and} \quad \mathbf{u} = \begin{pmatrix}u_{1} \\ u_{2} \\ \vdots \\ u_{n} \end{pmatrix}.\]Recall that we compute the inner product between \(\mathbf{v}\) and \(\mathbf{u}\) as
\[\mathbf{v}^{T}\mathbf{u} = v_{1}u_{1} + v_{2}u_{2} + \dots + v_{n}u_{n} = \sum_{i=1}^{n} v_{i}u_{i}.\]It turns out that this inner product is actually related to the angle between \(\mathbf{v}\) and \(\mathbf{u}\)! Let’s call this angle between the two vectors \(\theta\). Then we compute \(\cos(\theta)\) as follows
\[\cos(\theta) = \frac{\mathbf{v}^{T}\mathbf{u}}{\|\mathbf{v}\|_{2}\|\mathbf{u}\|_{2}}.\]In the formula above, \(\| \mathbf{v} \|_{2}\) is the length, or Euclidean norm, of \(\mathbf{v}\). Since \(\mathbf{v}\) and \(\mathbf{u}\) are arbitrary vectors, they might not have unit length (meaning that they might not have length equal to \(1\)). If we divide them by their lengths, however, then the normalized vectors \(\frac{\mathbf{v}}{\| \mathbf{v}\|_{2}}\) and \(\frac{\mathbf{u}}{\| \mathbf{u}\|_{2}}\) do have unit length!
Consider two vectors \(\mathbf{a}\) and \(\mathbf{b}\) on the unit circle (this means that they have length equal to \(1\)) as in the figure below.
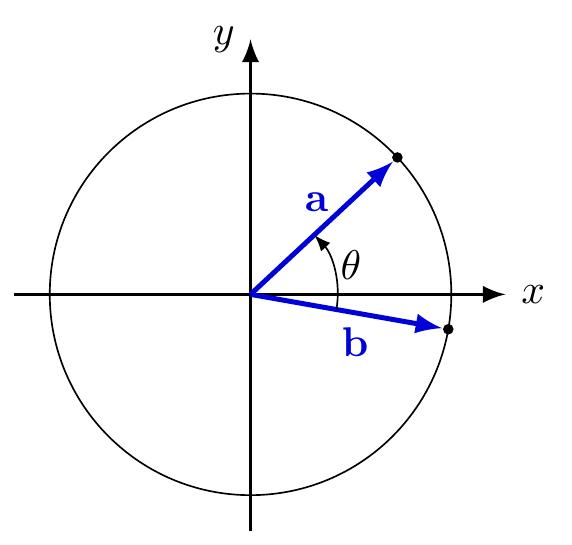
We can compute the angle \(\theta\) between \(\mathbf{a}\) and \(\mathbf{b}\) based on the formula above with
\[\theta = \arccos(\mathbf{a}^{T}\mathbf{b}).\]This is why we refer to \(\cos(\theta)\) as the cosine similarity. It gives us a sense of how close, or how similar, two vectors are to each other. For example, when they are very close to each other, then the angle \(\theta\) between them is very small. In this case, \(\cos(\theta)\) will be close to \(1\).
Putting it together in a simple recommender system
Now that we know how to tell how similar two vectors are to each other, we’re ready to code up a simple recommender system! Let’s write a function called recommend that takes in the following parameters: the standardized nutrition data matrix \(\mathbf{Z}\), the list of food item names items, and the index of our chosen food item our_index. Our recommend function will find and return the item in \(\mathbf{Z}\) that is most similar to our chosen food item.
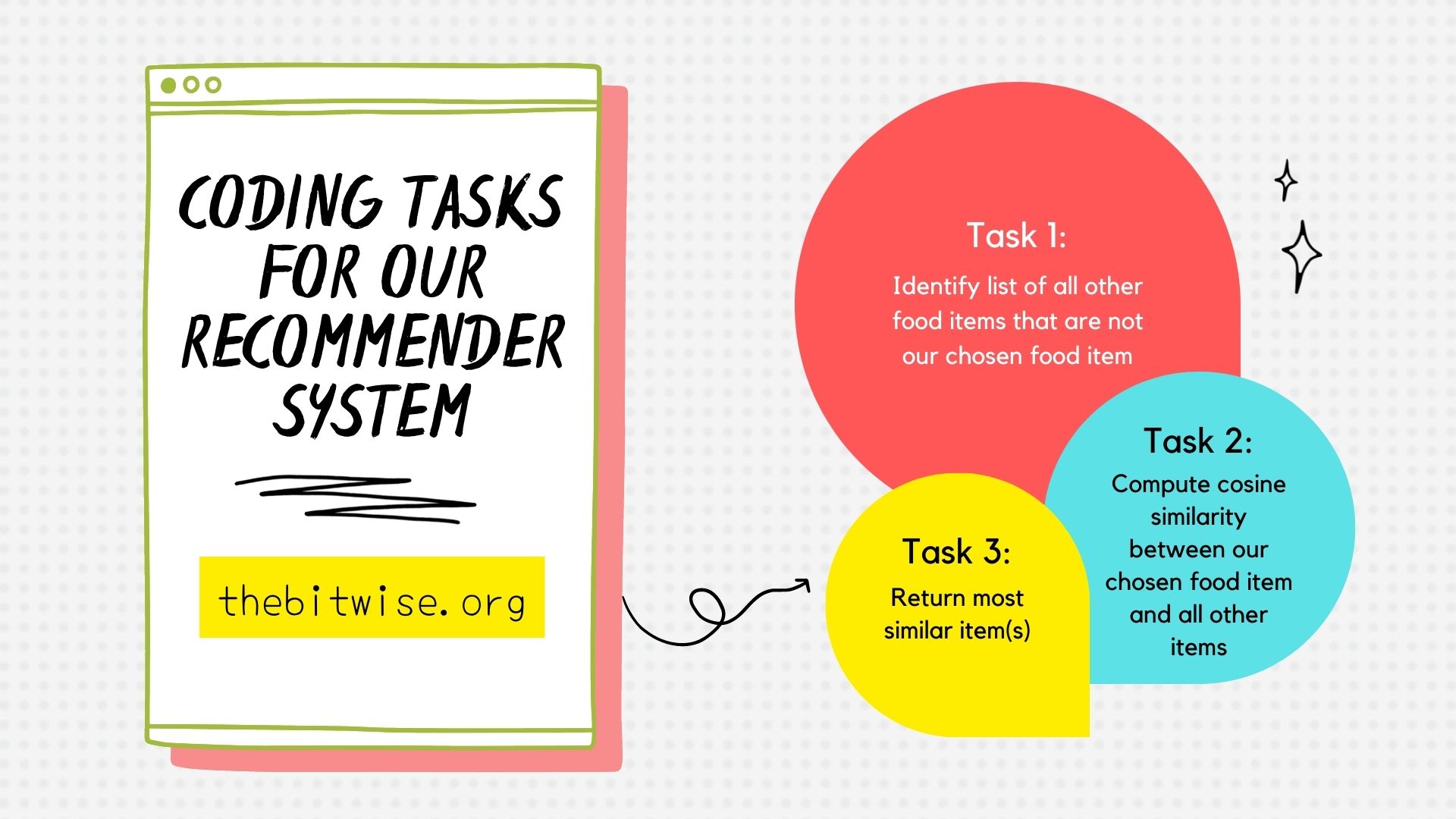
Let’s think through what things we’re going to need in this function! First, we’ll need to identify all the other food items in items that are not our chosen food item. We’ll also need to compute the cosine similarity between our chosen food item and all these other items in items. Finally, we’ll need to return the item with the largest cosine similarity to our chosen food item. If we store our computed cosine similarity values in a vector, we can find the largest item in that vector using the sort() function in R. We can read the help documentation in ?sort to see how to retrieve the indices of the sorted items.
Try this on your own first! How would you fill in the details for our recommend function?
#' Simple recommender system
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
recommend <- function(Z, items, our_index) {
# TRY THIS ON YOUR OWN FIRST
}Now let’s work on it together! Does your code look something the following?
#' Simple recommender system
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
recommend <- function(Z, items, our_index) {
# Get a list of all the other food items in `items`
other_items <- items[-our_index]
# Compute cosine similarity between our item and all other food items
cosSimilarity <- Z[our_index, ] %*% t(Z[-our_index,])
# Return most similar item to our chosen food item
return(as.character(other_items[sort(cosSimilarity, decreasing = TRUE,
index.return=TRUE)$ix[1]]))
}Let’s test out our recommend function! Which food item is most similar to “Big Mac”?
our_index <- get_index(items, "Big Mac")
recommend(Z, items, our_index)
#> [1] "Big Mac with Butter"Does this recommendation seem reasonable? Let’s try another item! Which food item is most similar to “Green Chile Bacon Burrito”?
our_index <- get_index(items, "Green Chile Bacon Burrito")
recommend(Z, items, our_index)
#> [1] "Green Chile Sausage Burrito"Modifications to our simple recommender system
Now that we’ve coded up a simple recommender system, let’s make some simple modifications to it! Let’s modify our recommend function to return the least similar item to our chosen food item! How would we do that?
Try this on your own first! How would you fill in the details for recommend_least_similar below?
#' Simple recommender system for least similar food items
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
recommend_least_similar <- function(Z, items, our_index) {
# TRY THIS ON YOUR OWN FIRST
}A quick look at the help documentation shows us that we can return the sorted indices in increasing order by setting decreasing = FALSE inside the sort() function. Does your code look something like the following?
#' Simple recommender system for least similar items
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
recommend_least_similar <- function(Z, items, our_index) {
# Get a list of all the other food items in `items`
other_items <- items[-our_index]
# Compute cosine similarity between our item and all other food items
cosSimilarity <- Z[our_index, ] %*% t(Z[-our_index,])
# Return least similar item to our chosen food item
return(as.character(other_items[sort(cosSimilarity, decreasing = FALSE,
index.return=TRUE)$ix[1]]))
}Let’s test this out! Which food item is least similar to “McChicken Biscuit”?
our_index <- get_index(items, "McChicken Biscuit")
recommend_least_similar(Z, items, our_index)
#> [1] "Green Chile Sausage Burrito"Which food item is least similar to “Big Breakfast with Hotcakes”?
our_index <- get_index(items, "Big Breakfast with Hotcakes")
recommend_least_similar(Z, items, our_index)
#> [1] "Chicken McNuggets (4 piece)"Let’s try another modification! Let’s modify our recommend function to return the top 5 most similar items! Try this on your own first! How would you fill in the details for recommend_top5 below?
#' Simple recommender system for top 5 most similar food items
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
recommend_top5 <- function(Z, items, our_index) {
# TRY THIS OUT ON YOUR OWN FIRST
}Does your code look something like the following?
#' Simple recommender system for top 5 most similar food items
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
recommend_top5 <- function(Z, items, our_index) {
# Get a list of all the other food items in `items`
other_items <- items[-our_index]
# Compute cosine similarity between our item and all other food items
cosSimilarity <- Z[our_index, ] %*% t(Z[-our_index,])
# Return top 5 most similar items to our chosen food item
return(as.character(other_items[sort(cosSimilarity, decreasing = TRUE,
index.return=TRUE)$ix[1:5]]))
}Let’s test this out! What are the top 5 most similar items to “Biscuit Sausage and Cheese”?
our_index <- get_index(items, "Biscuit Sausage and Cheese")
recommend_top5(Z, items, our_index)
#> [1] "Sausage Biscuit with Egg Whites"
#> [2] "Sausage Biscuit"
#> [3] "Big Breakfast with Egg Whites"
#> [4] "Sausage & Egg & Cheese McGriddles with Egg Whites"
#> [5] "Sausage McMuffin with Egg Whites"Does this recommendation seem reasonable? Let’s make one more modification! Let’s modify our recommend_top5 function to return the top \(k\) most similar items! Let’s try this on your own first! Which variable inputs would you need?
recommend_topk <- function() {
# TRY THIS ON YOUR OWN FIRST
}Let’s work on this together! We’ll need to add an input k for the number of similar items we want to return.
Does your code look something like the following?
#' Simple recommender system for top k most similar food items
#'
#' @param Z data matrix
#' @param items Names of food items
#' @param our_index Index of our chosen food item
#' @param k Number of top similar items to return
recommend_topk <- function(Z, items, our_index, k) {
# Get a list of all the other food items in `items`
other_items <- items[-our_index]
# Compute cosine similarity between our item and all other food items
cosSimilarity <- Z[our_index, ] %*% t(Z[-our_index,])
# Return top k most similar items to our chosen food item
return(as.character(other_items[sort(cosSimilarity, decreasing = TRUE,
index.return=TRUE)$ix[1:k]]))
}Let’s test this out! Which are the top 3 most similar items to “Blueberry Muffin”?
our_index <- get_index(items, "Blueberry Muffin")
recommend_topk(Z, items, our_index, 3)
#> [1] "Cranberry Orange Muffin"
#> [2] "Blueberry Muffin Main Street Gourmet"
#> [3] "Cinnamon Melts"Does this output seem reasonable? Let’s try one more! Which items are the top 7 most similar items to “Apple Cinnamon Muffin”?
our_index <- get_index(items, "Apple Cinnamon Muffin")
recommend_topk(Z, items, our_index, 7)
#> [1] "Fruit & Maple Oatmeal"
#> [2] "Fruit and Maple Oatmeal with Maple Sugar Packet"
#> [3] "Fruit & Maple Oatmeal without Brown Sugar"
#> [4] "Fruit N Yogurt Parfait"
#> [5] "Cranberry Orange Muffin"
#> [6] "Blueberry Muffin"
#> [7] "Blueberry Muffin Main Street Gourmet"Great job!

In this Code Lab, we coded a simple recommender system using cosine similarity. We tested our recommender system on a small dataset of food items from McDonald’s. In the process, we got some more practice on working with vectors, Euclidean norms, and inner products from our our post on getting started with linear algebra in R. We also got more practice with writing functions and for loops, and using the sort() function. Finally, we learned about the relationship between angles between vectors and their inner product. We also learned how to standardize variables and normalize observations! Great job!




